O que é a gestão?

É o processo de coordenar as actividades de forma a que elas sejam desempenhadas de forma eficiente e eficaz, com e através de outras pessoas.

Eficiência
Conseguir o máximo de Output (por exemplo produção) com o mínimo de Inputs (no caso, de recursos).
“Doing the things right”
Focaliza-se nos meios. Uma elevada eficiência significa um baixo desperdiço de meios e recursos.

Eficácia
Consiste em executar as actividades de tal modo que os objectivos sejam alcançados.
“Doing the right things”
Focaliza-se nos fins.
Assim, o desafio numa Gestão é portanto que ela seja Eficaz e Eficiente.

Processo
Representa a sequência de funções ou actividades primárias desempenhadas pelos gestores. Exemplo: A -->B -->C -->D -->E

Coordenar
Consiste em tomar decisões quanto à afectação dos recursos.
Distingue uma posição de gestão de uma que não é.

Fonte: Introdução à Gestão, Elaborado tendo por base as aulas do Professor José Taborda Farinha

NIVEIS DE GESTÃO

Nas empresas existem diferentes níveis de gestão, pois os gestores também podem ser geridos.

Gestores de Primeira Linha (First Line Managers) – Gerem o trabalho dos não gestores, que estão directamente envolvidos com a produção e criação dos produtos da organização.

Gestores Intermédios (Middle Managers) – Todos os gestores situados entre os gestores de Primeira linha e os gestores de topo. Gerem os gestores de Primeira linha

Gestores de Topo (Top Managers) – Responsáveis pelas decisões que envolvem toda a organização e pelo estabelecimento dos planos e dos objectivos para a totalidade da organização. Têm assim a responsabilidade máxima na empresa.

Quando uma empresa é dirigida por um Conselho de Administração, e não simplesmente por um Director Geral, é dirigida pelo chamado Board of Directors, sendo o seu elemento que mais dá a cara o C.E.O. ou seja, o Chief Executive Officer.

O processo de tomada de decisão faz parte das quatro funções da gestão. É por isso que os gestores são, frequentemente, chamados “decision makers”.

Fonte: Introdução à Gestão, Elaborado tendo por base as aulas do Professor José Taborda Farinha

Planeamento Níveis de Gestão e Objectivos

O planeamento envolve a definição dos objectivos da organização, estabelecendo a estratégia global (que pode ser definida como o conjunto de caminhos seguidos pela empresa para alcançar os objectivos), e o desenvolvimento de planos para integrar e coordenar as actividades da organização.
Existem 2 tipos de Planeamento:

Planeamento Informal – não é escrito, e tem como características uma reduzida partilha dos objectivos, e o facto de ser genérico e com ausência de continuidade.

Planeamento Formal – É escrito. Tem como características o facto de definir objectivos específicos, e programas de acção para alcançar esses mesmos objectivos.


Tipos de Objectivos

Objectivos Estratégicos – Envolvem toda a organização ou cada uma das suas áreas de negócios, a médio e longo prazo.

Objectivos Tácticos – Situam-se a nível intermédio da organização. Ex: Marketing ou Comunicação com horizonte de médio e curto prazo.

Objectivos Operacionais – Definem-se ao nível de gestão da primeira linha e com horizonte de curto prazo.

Planos Estratégicos: Aplicam-se a toda a organização e a cada uma das suas áreas de negócios, a médio e longo prazo. Estabelece os objectivos estratégicos e procura posicionar a organização em termos do seu “environment”.

Planos Tácticos e Operacionais: Especificam os detalhes de como os objectivos tácticos e operacionais serão alcançados. Na prática, os planos práticos e operacionais estão juntos nas empresas, daí se falarem em apenas dois tipos de planos. Estes cobrem um horizontal temporal de curto prazo.

O plano estratégico é direccional, ao passo que os planos operacionais o tornam específico.

Planos Direccionais – Planos flexíveis que definem “guidelines” gerais, focalizados sem limitar os cursos de acção.

Planos Específicos – Detalhados definindo com pormenor os cursos de acção.

Planos de Uso Único – Desenhados para satisfazer as necessidades de uma situação única.

Planos de Continuidade – Fornecem orientação para actividades repetitivas, e incluem políticas, procedimentos e regras.

Fonte: Introdução à Gestão, Elaborado tendo por base as aulas do Professor José Taborda Farinha

Tipos de Problemas e Decisões

Problemas Bem Estruturados e Decisões Programadas

Problemas Bem Estruturados são problemas lineares, familiares e facilmente definidos.

Como resposta a este tipo de problemas o gestor utiliza Decisões Programadas, ou seja, uma decisão repetitiva facilmente aplicável ao problema em causa.

Através da decisão programada, será reduzido o número de alternativas para a solução do problema, facilitando a eficiência organizacional. Estas decisões programadas levam aplicação de um procedimento, regra ou política.

Procedimento – série de passos interrelacionados e sequenciais usados para responder a um problema estruturado, a única dificuldade reside em identificar o problema pois uma vez identificado o procedimento é aplicado.

Regra – declaração explícita do que fazer ou não fazer.

Política – orientação ou parâmetros para a tomada de decisões, contém termos ambíguos ficando a interpretação por conta do decisor.

Problemas Não Estruturados e Decisões Não Programadas

Problemas Não Estruturados, são problemas novos para os quais a informação é ambígua e incompleta. Para fazer face a estes problemas existem as Decisões Não Programadas, que produzem uma resposta customizada e única. Estes são mais frequentes entre os gestores de nível mais elevado.

Convém salientar, que são poucas as decisões na vida real que são totalmente programadas ou não programadas, pois estes constituem casos extremos, sendo que as decisões se situam, essencialmente, algures entre estas.

Fonte: Introdução à Gestão, Elaborado tendo por base as aulas do Professor José Taborda Farinha

Estilos Na Tomada de Decisão

Existem duas dimensões que definem a perspectiva de tomada de decisões:

Forma de pensamento – que vai de Racional a Intuitivo

Tolerância para a ambiguidade – está relacionada com o número de alternativas tomadas em simultâneo, bem como a sua consistência, o seu ordenamento.

Existem quatro estilos na tomada de decisões:

Directivo – Rápido, eficiente e lógico;
Analítico – Cuidadoso e capaz de se adaptar ou enfrentar novas situações;
Conceptual – Capacidade de encontrar soluções criativas;
Comportamental – Procura aceitação das decisões.

Fonte: Introdução à Gestão, Elaborado tendo por base as aulas do Professor José Taborda Farinha

Funções

FUNÇÕES lINEARES

As funções da forma f(x) = kx são chamadas funções lineares ou funções de proporcionalidade, onde k é uma constante numérica e nos dá o declive da recta. O gráfico deste tipo de funções é uma recta que passa pelo centro de coordenadas (0,0).

Uma aplicação desta funcao á àrea da gestão poderia ser o exemplo da venda de gelados, se as vendas fossem mais elevadas nos dias quentes do que nos dias frios, poderiamos dizer que as vendas estavam positivamente correlacionadas com a temperatura. Se iguais alterações na temperatura produzirem, aproximadamente, iguais alterações nas vendas, entao a correlação diz-se linear e a relação pode ser representada por uma linha recta num gráfico.
Outras aplicações poderiam ser o desenvolvimento de um produto o que tem consequências de primeira ordem na área de marketing e de produção. Os investimentos em novos equipamentos e processos o que irá influenciar directamente a qualidade. A promoção de funcionários para cargos de liderança irá influenciar a estratégia e o clima organizacional.

Função Receita

É directamente proporcional à quantidade vendida. É entendida como sendo o produto entre o preço de venda (p), pela quantidade vendida (q). R = p.q

Na atividade operacional de uma empresa, há diversos fatores contribuem para a formação da receita proveniente do volume de vendas. Fatores como o volume de produção e o potêncial do mercado não podem ser esquecidos para a formação da receita, porém, em pequenos intervalos onde já foram consideradas as variáveis restritivas e considerando-se o preço constante, nesse intervalo de produção, o rendimento total da empresa será função somente da quantidade vendida.

Por exemplo, uma empresa de producao de caixas registradoras, que as vende a 80,00€ cada, se não for vendida unidade alguma, a Receita será 0; se forem vendidas 100.000 unidades, o rendimento total (receita total) será 8 milhões de euros.

Vê-se então que a função receita pode ser uma função linear cujo gráfico é uma recta que passa pela origem e tem como declive o preço de venda (por unidade). No caso da Receita ser uma função linear (preço constante), a equação que define a função é R(q) = p.q onde R é a receita total (rendimento total), p é o preço por unidade do produto e q é a quantidade vendida. Como p > 0, o gráfico é do tipo:

Obs.1: Se p (preço) é fixo, R é uma função linear da quantidade vendida. Porém se o preço é dado pela equação da procura de um bem, a equação da receita não será linear. Nesse caso R(q) = f(q).q, onde p = f (q) é a função preço da procura.

FUNÇÃO QUADRÁTICA

Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0.

A função Lucro é um exemplo de uma função quadrática, isto é de uma função que pode ser escrita na forma, f(x) = ax2 + bx + c onde a , b e c são números reais quaisquer e a diferente de zero.

Grandes vendas não significam necessariamente, lucros maiores. O gráfico da função L mostra que se o nível de produção estiver entre A e V', quantas mais unidades produzidas maior será o lucro obtido. Se, no entanto, o nível de produção estiver entre V' e B aumentar a produção significa diminuir o lucro.

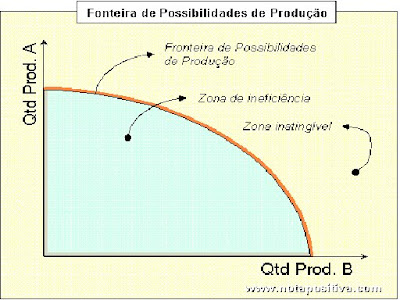
Fronteira de Possibilidades de Produção

A fronteira de possibilidades de produção representa as quantidades máximas de produção que podem ser conseguidas numa determinada economia dadas as tecnologias e as quantidades dos factores produtivos de que dispõe.

Devido às limitações de recursos e de tecnologias, as quantidades de produção também são limitadas. Numa economia imaginária em que sejam produzidos apenas dois bens, se todos os recursos fossem utilizados para produzir um deles, conseguir-se-ia produzir uma determinada quantidade máxima desse mesmo bem e nada do outro. De igual forma, se os recursos fossem transferidos na sua totalidade para o outro bem, seria conseguida uma determinada quantidade máxima de produção desse mesmo bem e não se produziria nada do primeiro. Além destas duas possibilidades extremas, existem inúmeras situações intermédias de repartição dos recursos para a produção dos dois bens e que resultam em diferentes quantidades máximas de produção de cada um deles.

Para facilitar a sua compreensão, a fronteira de possibilidades de produção pode ser representada num gráfico. Para isso, em cada um dos eixos é representada a quantidade de cada um dos bens: o conjunto de todos os pontos máximos de produção representa a fronteira de possibilidades de produção; os pontos exteriores à fronteira de possibilidades de produção são inatingíveis dadas a tecnologia e a quantidade de factores produtivos disponíveis; pontos interiores representam ineficiência produtiva, ou seja, quantidades que estão abaixo das possibilidades da economia.

FUNÇÃO LOGARITMICA

Chama-se logaritmo de um número x na base a (a > 0 e a ≠ 1), ao número a que é necessário elevar a base a para obter x e escreve-se loga x = y <=> ay = x, ou seja, o logaritmo de um número, numa dada base, é o expoente a que é preciso elevar a base para obter o número.

Temos então que o loga x = y <=> x = a log x <=> loga ay = y